Nom : |
|
Classe : |
Prénom : |
|
Date : |
1) Taper :
AV 80 TD 30 RE 80 TD 30
On obtient la figure suivante :
En tapant deux fois cette ligne d'instruction :
AV 80 TD 30 RE 80 TD 30
AV 80 TD 30 RE 80 TD 30
On obtient alors :
Le but est de fermer cette figure pour obtenir une "étoile".
Taper :
REPETE 3
AV 80 TD 30 RE 80 TD 30
FIN REPETE
Obtient-on une étoile ?
......................................................................................
Combien de fois au minimum faut-il répéter les instructions "AV 80 TD 30 RE 80 TD 30" pour obtenir une étoile ?
......................................................................................
2) On change maintenant l'angle dans les instructions TD.
Commencer par modifier le programme précédent par :
REPETE 1
AV 80 TD 40 RE 80 TD 40
FIN REPETE
Quel est le nombre minimum de répétitions nécessaires pour fermer la figure ?
.....................................................................................
Compléter alors le tableau suivant :
A (angle en degrés) |
10 |
15 |
18 |
30 |
36 |
40 |
45 |
50 |
n (Nombre minimum de répétitions) |
|
|
|
|
|
|
|
|
Ang (angle total en degrés) |
|
|
|
|
|
|
|
|
Rq : l'angle total est obtenu en multipliant l'angle A par le nombre minimum de répétitions n (Ang = n 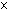 A) A)
En examinant le tableau ci-dessus, que peut-on émettre comme conjecture pour l'angle total ?
..................................................................
Avec cette conjecture, compléter l'égalité suivante :
.Ang = k 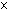 .................... (k entier naturel) .................... (k entier naturel)
Il semble donc que pour obtenir une étoile, si p est le nombre de répétitions (compléter l'inégalité) :
p 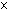 ............. = k ............. = k 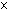 ............ ............
Étoile obtenue pour un angle de 50°
|
|

|
|